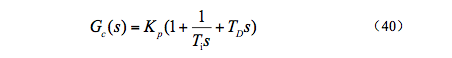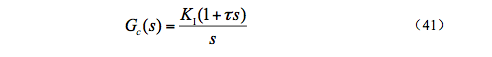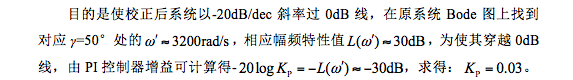4.4 Buck变换器的PI控制器频域设计方法
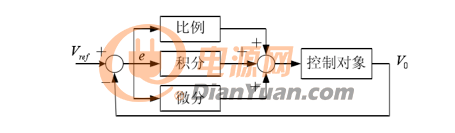
实际应用中,最广泛的控制器为比例(P),积分(I),微分(D)控制,简称PID控制。这是一种线性控制方法,它通过设定值和实际值产生偏差,将偏差的比例、积分、微分通过线性组合构成控制量,对被控对象进行控制。
图15 PID控制器原理图
其传递函数可表示为:
在上式中,Ti为积分时间常数,TD为微分时间常数。
在比例,积分,微分三个控制因子中,比例控制能迅速反应误差,但比例控制不能消除稳态误差,且比例系数的增大会引起系统不稳定;积分控制的作用是:只要系统存在误差,积分控制作用就不断的积累,输出控制量控制误差,故只要有足够的时间,积分控制就能完全消除误差,积分作用太强会使系统超调加大,甚至使系统出现振荡;微分控制可以反映偏差信号的变化趋势,减小超调量,克服振荡,使系统的稳定性提高,同时加快系统的动态响应速度,减小调整时间,从而改善系统动态性能。实际控制过程中,往往根据系统性能指标的要求采用不同的组合校正方式,如PI、PD、PID等。
对于Buck变换器采用PI控制,从频率特性角度看PI控制实质上相当于滞后校正。由式(44),令TD=0,可得典型PI调节器的传递函数为
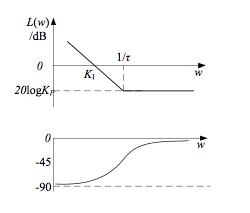
式中 , ,PI控制器的对数频率特性曲线如图16所示
图16 PI控制器幅频特性曲线
转折频率为 ,增益为-20logKP。因为PI控制器作用原理相当于滞后校正,参数设计可按串联滞后环节原则确定。在上一小节原系统Bode图分析中可知,高频段以斜率为-40dB/dec穿越0dB线,且相角裕量Pm≈4°。加入PI校正环节之后,目的是要增大相角裕量,校正环节的转折频率 使校正后的系统具有新的截止频率,并且以-20dB/dec斜率过0dB线。按照以下步骤设计PI控制器参数。
(1)确定校正后系统相角裕量;
按稳定系统相角裕量为45°的原则,并考虑留有一定裕量,取γ=50°,使校正后系统相角裕量约为50°。
(2)确定PI控制器参数 ;
(3)确定PI控制器参数K1 ;
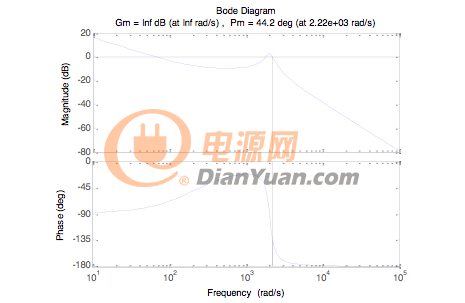
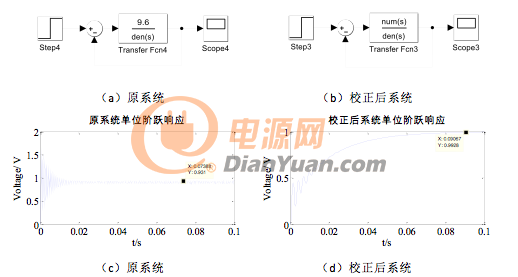
校正后系统的Bode图如图17所示为,可以看出相角裕度为44.2°满足要求。为了对比PI控制器对Buck变换器的控制效果,以下分别观察原系统和加PI控制器校正后系统的单位阶跃响应,Matlab/Simulink仿真模型如图18(a)(b)所示,单位阶跃响应如图18(c)(d)所示。可以看出原系统是稳定的,但存在较大的输出超调,且一直处于振荡状态,且输出平均值小于设定值1,存在误差;而校正后的系统无超调且振荡减少,稳定后,值为1,但是有较长的调节时间,主要是由于PI参数还未达最优值,需要进一步调节PI参数。另外一个原因是由于PI控制器本身就是一个滞后环节,通过牺牲系统的快速性而获得高的稳态性能。
图17 校正后系统Bode图
图18 单位阶跃响应仿真框图及结果